Advanced-Programming

Haskell

Slides:

Data types

data Color = Red | Yellow | Blue

data Tree = Leaf Int | Node (Int, Tree, Tree)

Case expressions

case t of
  Leaf n -> ...
  Node(n, lt, rt) -> ...

Function types

f :: A -> B means for every x ∈ A, if f(x) terminates, then f(x) ∈ B.

Higher order functions

Any curried function with more than one argument is higher-order: applied to one argument it returns a function.

From functional to stream-like

length(tail(reverse [1,2,3])) => 2

becomes

[1,2,3] |> reverse |> tail |> length => 2

Map

Applies argument function to each element in a collection.

map (+1) [1,2,3] => [2,3,4]

Filter

Takes a collection and a boolean predicate, and returns the collection of the elements satisfying the predicate.

filter even [1..10] => [2,4,6,8,10]

Reduce

foldl, foldr, foldl', foldl1 etc.

sum' xs = foldl (\acc x -> acc + x) 0 xs

The difference between foldl and foldr is that the first start from the top, so is applicable also to infinite lists, the second one requires a finite list.

The difference between foldl and foldl' is that the second one uses tail-recursion (see below) and for that reason is more performant.

Recursion

Iteration and recursion are equally powerful in theoretical sense. Anyway, in general a procedure call is much more expensive than a conditional branch, thus recursion is in general less efficient.

Tail recursive functions

Non tail-recursive

int rfun() {
  ...
  return 1+rfun();
}

Tail recursive

int trfun() {
  ...
  return trfun();
}

Example

Quadratic, non tail recursive

reverse [] = []
reverse (x:xs) = (reverse xs) ++ [x]

Can be rewritten with tail-recursion in linear time

reverse xs =
  let rev ([], accum) = accum
      rev (y:ys, accum) = rev (ys, y:accum)
  in rev (xs, [])

Type classes

Provide concise types to describe overloaded functions.

Allow users to define functions using overloaded operations and to declare new collections of overloaded functions.

A type class declaration defines a set of operations and gives the set a name.
Example: Eq a type class defines the operations == and \= with type a -> a -> Bool.
Usage: member:: Eq w => w -> [w] -> Bool.

Default type classes

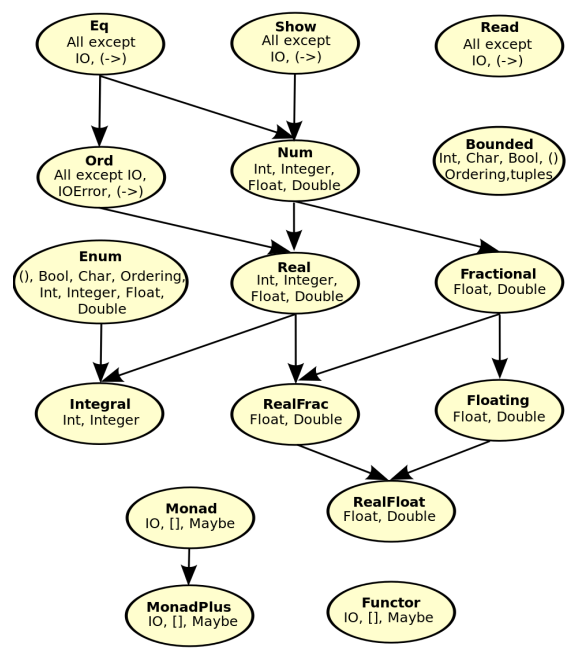
Eq: equality
Ord: comparison
Num: numerical operations
Show: convert to string
Read: convert from string
Enum: operations on sequentially ordered types

Type classes hierarchy

Declaration

The class declaration says what the Num operations are.

class Num a where
  (+) :: a -> a -> a
  (*) :: a -> a -> a
  negate :: a -> a
  ...

Instance

An instance declaration for a type Int says how the Num operations are implemented on Int’s.

instance Num Int where
  a + b = intPlus a b
  a * b = intTimes a b
  negate a = intNeg a
  ...

Default methods

Type classes can define default methods. Instance declaration can still override it by providing a more specific definition. If an instance declaration doesn’t provide a method implementation, the default one is applied.

class Eq a where
  (==) :: a -> a -> Bool
  x == y = not (x /= y)

  (/=) :: a -> a -> Bool
  x /= y = not (x == y)

If is not necessary to override the default definition, deriving can be used.

Deriving

For Read, Show, Bounded, Enum, Eq and Ord the compiler can generate instance declaration automatically.

data Color = Red | Green | Blue
  deriving (Show, Read, Eq, Ord)

Under the hood

This

square :: Num n => n -> n
square x = x * x

is compiled into this

square :: Num n -> n -> n
square d x = (*) d x x

where the extra value argument d of the function is a value of data type Num n and represents a dictionary of the required operations.

Furthermore, the compiler converts each type class declaration into a dictionary type declaration and a set of selector functions. In other words, this

instance Num Int where
  a + b = intPlus a b
  a * b = intTimes a b
  negate a = intNeg a
  ...

is compiled into this

dNumInt :: Num Int
dNumInt = MkNum intPlus
                intTimes
                intNeg
                ...

Compositionally

sumSq :: Num n => n -> n -> n
sumSq x y = square x + square y

becomes

sumSq :: Num n -> n -> n -> n
sumSq d x y = (+) d (square d x) (square d y)

Functor

A type class where the predicate is over a type constructors rather than on a type.

Example:

instance Functor Tree where
  fmap f (Leaf x) = Leaf (f x)
  fmap f (Node(t1,t2)) = Node(fmap f t1, fmap f t2)

Monads

Constructor classes (type constructor) introducing operations for “putting a value into a box” (return) and compose functions that return “boxed” values (bind: x >>= y).

(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b

Functors with fmap allow to apply functions inside “boxes”.

Haskell monads

Maybe
Error
State
IO
lists ([])
Reader
Writer

Maybe

data Maybe a = Nothing | Just a

A value of type Maybe a is a possibly undefined value of type a.
A function f :: a -> Maybe b is a partial function from a to b.

Main

main::[Response] -> [Request]

IO

IO is a type constructor, instance of Monad. A value of type IO t is a computation or “action” that, when performed, may do some input/output before delivering a result of type t.

return returns the value without making I/O
Then (>>) and bind (>>=) composes two actions sequentially into a larger action.

(>>=) :: IO a -> (a -> IO b) -> IO b

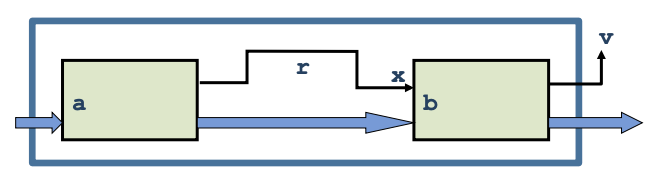
Bind scheme

Binds the result of the left-hand action in the action on the right.

Evaluating an action has no effect, performing the action has the effect.
The only way to perform an action is to call it at some point, directly or indirectly, from Main.main.

This site is open source. Improve this page.